前言: 本文只讲解原理, 不讲解BloomFilter中各项指标的公式的推算, 能让你知道有这么一个东西(what), 他能达到什么效果(why), 是如何做到的(how).
(What)
Bloom Filter 是用一个 位数组(数组的每个元素不是1就是0) 来表示一个大的元素集合, 而且通过这个数组就可以判断某个元素是不是属于这个集合
大大节省了空间, 但是有代价的, 就是有一定的错误率(为什么会有, 后面举个例说明一下)
假定我们有一个已知的集合, S = {a1, a2, … , an} (这里的元素不仅仅是数字, 而是泛指所有对象), 我们要判断一个元素 x 是否属于这个集合, 普通的做法有两种形式:
1. 遍历 比较, 性能和S的大小成反比 (时间问题)
2. hash+链表(传说中的hashMap), 速度较快, 但是要把集合的所有数据都存进内存 (空间问题)
在性能要求高, 而且空间不足的情况下, BloomFilter就派上用场了
(Why)
BloomFilter能解决什么问题?
以少量的内存空间判断一个 元素 是否属于这个集合, 代价是有一定的错误率
(How)
工作原理
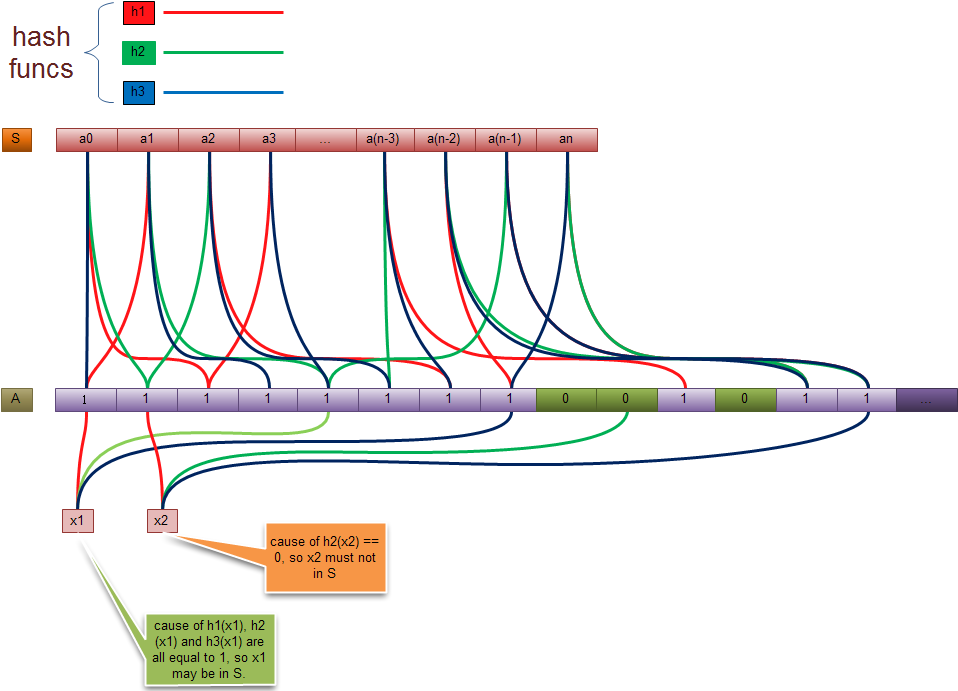
1. 初始化一个数组, 所有位标为0, A={x1, x2, x3,…,xm} (x1, x2, x3,…,xm 初始为0)
2. 将已知集合S中的每一个数组, 按以下方式映射到A中
2.0 选取n个互相独立的hash函数 h1, h2, … hk
2.1 将元素通过以上hash函数得到一组索引值 h1(xi), h2(xi),…,hk(xi)
2.2 将集合A中的上述索引值标记为1(如果不同元素有重复, 则重复覆盖为1, 这是一个觅等操作)
3. 对于一个元素x, 将其根据2.0中选取的hash函数, 进行hash, 得到一组索引值 h1(x), h2(x), …,hk(x)
如果集合A中的这些索引位置上的值都是1, 表示这个元素属于集合S, 否则则不属于S
几个前提
1. hash函数的计算不能性能太差, 否则得不偿失
2. 任意两个hash函数之间必须是独立的.
即任意两个hash函数不存在单一相关性, 否则hash到其中一个索引上的元素也必定会hash到另一个相关的索引上, 这样多个hash没有意义
错误率
工作原理的第3步, 的出来的结论, 一个是绝对靠谱的, 一个是不能100%靠谱的.
如果集合A中的这些索引位置上的值都是1, 表示这个元素属于集合S, 否则则不属于S 标红的这句话是绝对靠谱的.
至于错误率有多大, 我这里不想去推算, 后面会给出参考文章, 不在本文的讨论范围, 很简单就能举个例子说明错误率是存在的
当A长度不是很大时, 很容易出现一种情况, 使得A上的元素全部被标记为1了, 这时所有的元素都会被认为是S里的元素, 所以, 错误率是存在的!
(可以看出, 错误的大小跟A的长度以及hash函数的个数有关)
(In Action)
应用
1. 假如你有一个很大的商品库(亿级别), 然后你要做一个浏览型的网站, 这时候, 你不可能把所有的商品都丢给用户去浏览, 而是从商品中挑选出部分属于“精品”的商品来给用户浏览, 提高用户体验和转化率, 你对你的精品库建立一套搜索引擎2. 由于互动需要, 你需要对你维护的精品库的商品数据实时更新动态, 比如XXX在某时间给了一个”好评”, “购买了一笔”, “赞”,”喜欢”等等3. 为了实现这种实时更新, 你通过MQ订阅了商品相关的消息(notify)(交易, 评价, SNS), 只要商品发生动态就会发送给你的系统.4. 这时候, 由于全网的商品很多, 发生动态的消息很多情况下是跟你的精品库没有关系的, 这时候你需要挡掉这些消息, 不进行处理.5. 此时, 不可能每来一个商品数据你先通过搜索引擎判断一下商品不是在你的精品库内(效率问题, 压力问题), 这时候, bloomFilter派送用场了.6. 从上面错误率的点, 我们可以看到, 如果一个元素被BloomFilter判断为不属于原有的集合, 那么这个元素是肯定不属于这个集合的(被排除的准确率是100%的)通过bloomfilter的几项指标, 就可以挡掉大多数没有相关的数据, 而只处理有关系(虽然有部分无关)的数据了.
(Graphics)附图一张
参考文章:
幂等