非对称加密算法

前言

目前主流的非对称加密算法主要有几类：RSA、DHKE、Elliptic Curve。

虽然大类分成这几类，实际上他们底层的原理都是依赖于素数和同余原理来做的。素数是除了他本身和1以外，无法被其他任何正整数整除的数字。这样的数字有多少呢？无穷个。我们知道，一个数字的因式分解，最终都能分解成n个素数的相乘，由于素数有无穷多个，也就意味着一些巨大的数是很难分解的，特别是两个大的素数（例如几百位、上千位）的乘积就更难因式分解了，催生了很多在理论上不可行，但在经济上可行的加解密算法。为什么说是理论上不可行呢？因为数字再大，只要有恒心（例如几百年、上千年甚至几百亿年）总能把一个大数因式分解，也就是基本假设不成立，一旦能因式分解，所有的这类密码都将被破解。经济上可行是因为，因式分解一个这样的大数字花费的经济成本（计算机、电力等）太高，以至于不会有人去尝试暴力破解。当然，据说有可以破解这类的量子算法，基于量子计算机多维度并发计算，还是有机会的。目前量子计算机造价昂贵且还没有大规模商用，用于破解这类的密码成本也是相当高的，暂时还是安全的。对应的策略是，a：发明后量子加密算法，在量子计算机流行之后也能用后量子算法来加解密，保障量子计算机破解不了这类的密码；b：用量子纠缠实现通信，可以完全杜绝中间人攻击，此时密钥不是最重要的了。目前美国为主的西方国家主要在主导后量子密码学，而我国科学家更多在主导量子通信。

下面我会用相对易懂的预言推导一下这几类算法的原理，一些不太好理解的定理，不会太深入去推导。

1、RSA非对称加解密的基本原理

a）基本假设与前提：两个大素数的乘积无法（轻易地）被因式分解
b）算法实现：
1）随机生成两个大的素数，p、q
2）令 n = p * q，另 N = （p-1) * (q-1)
3）从 在 (1, n-1）区间内，找到一个随机数d
4）找到一个 e，满足 e * d ≡ 1 mod N

此时，d 与 n 结合就形成了私钥，记为 pubk = (d,n); e 与 n 结合形成私钥，记为 priv = (e, n)
假设有消息m
公钥加密过程，E(m) = m^e % n => 密文记为 c
私钥解密过程，D(c) = c^d % n =(m^e)^d % n = m^(ed) % n
由于 e * d ≡ 1 mod N, 所以 D(c) = m^(ed) % n = m ^ (1 mod N) % n = m % n (同余定理）
ed ≡ 1 mod (p-1) * (q-1) , 由于 p-1 与 q – 1 分别与 n 互质 （最大公约数为1）， 所以 m ^ (ed) % n ≡ m ^ (1 % (q-1)*(p-1)) % n ≡ m % n (这句推导很魔幻，我看不懂，但大受震撼） , 从而解密过程无需知道p、q就能解密得到原文m。

示例代码可以从我的gist中找到，地址（https://gist.github.com/jiacheo/c01ca88ee308a8fe8293452cc71fdcb5)

2、DHKE 密钥交换的基本原理

DHKE严格上讲其实不是非对称加密算法，因为这个算法是通过非对称的方式来交换密钥，而最终通信双方使用相同的密钥来做对称的加解密。

算法原理如下：

先约定两个所有人都知道的素数 p、g，其中 p > g
通信双方，假设为A和B
A生成一个随机数a，B生成一个随机数b
A本地计算 d1 = g^a mod p
B本地计算 d2= g^b mod p
AB交换d1，d2（这时d1、d2可能被第三方窃取，但没关系）
A拿到d2计算 s = d2 ^ a mod p
B 拿到 d1 计算 s` = d1 ^ b mod p

可以看出 s = d2 ^ a mod p = (g ^ b) ^ a mod p = g^ab mod p
s` = d1 ^ b mod p = (g ^ b ) ^ a mod p = g ^ ab mod p == s

也就是A、B双方共同拿到了密钥s，后续通信可以通过s来进行。
假设中间有AB交换d1/d2的时候被窃取了，由于窃取的人不知道 a和b、所以无法计算出s，也就无法知道他们约定的密钥是什么了。

示例代码也可以从我的gist中找到，地址（https://gist.github.com/jiacheo/3dd14d4be509fb7f945b926cf237a921）

3、Elliptic Curve 椭圆曲线非对称加密的基本原理

a) 首先，先弄明白什么是椭圆曲线。

椭圆曲线是诸如 y2 = ax3 + bx + c 的一条曲线，其中a、b、c为常数。例如比特币的签名认证算法选用的就是 y2 = x3 + 7 的曲线，该曲线画出来大致长这样：

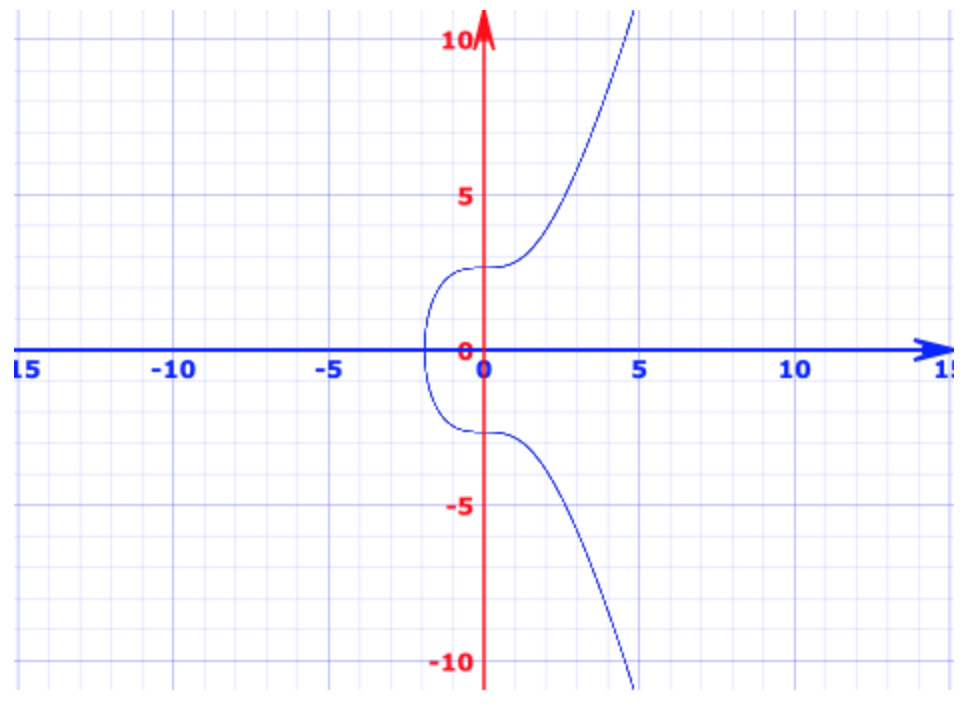
该曲线有以下特性（推导过程省略，知道他有这些特性就行了）

1）曲线是关于x轴对称的。
2）对曲线上任意两个非对称点做一条直线，该直线一定会和曲线相交与某一点
3）对曲线上任意一点（y = 0的点除外）做切线，该切线一定会和曲线相交与某一点

b）知道了曲线，我们定义一下曲线上的加法

已知曲线上的任意两点P、Q，其中P和Q非对称，那么P + Q的结果就是特性 2) 中连接这两点的直线与曲线相交的那一个点R`关于x轴对称的点R，记为 R = P + Q。特殊情况下，P 和 G 为同一点时，引用特性 3) 的切线相交点R`关于x周对称的点R，记为 R = P + Q = P + P = Q + Q = 2P = 2Q

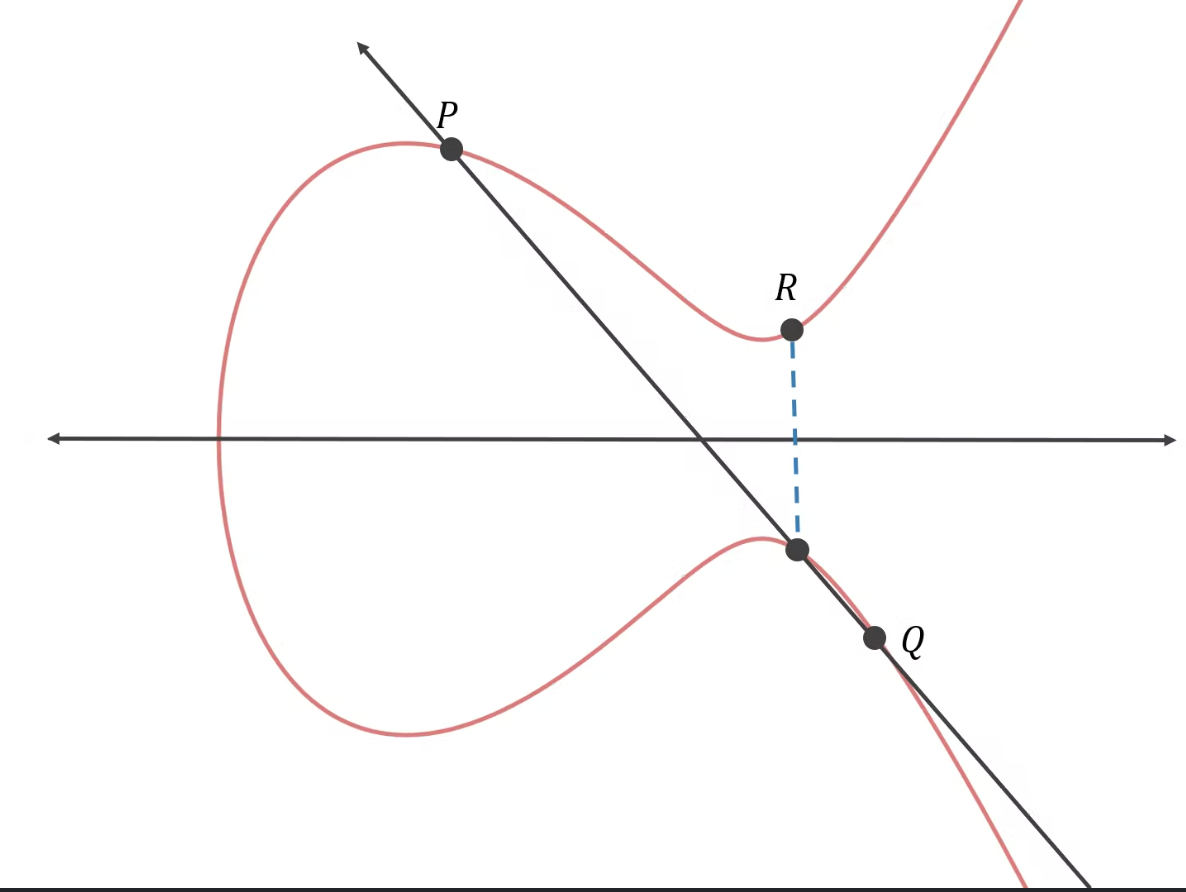
所以这里也定义了乘法，乘法不是点和点相乘，而是系数和点相乘，代表这个点加了多少次。 x * P 代表 P点加了x次。
其中乘法（点乘）满足 分配律(和结合律），即 (a + b) * P = aP + bP ，例如： 4P = (2+2) * P = 2P + 2P

c）接下来定义私钥和公钥

我们选一个公众已知的点G，称作为基点。私钥是一个随机整数 x， 公钥则为 X = x * G。 即公钥就是 将基点相加了 x次。 目前已经证明，通过私钥x和基点G推导出公钥X是非常迅速的，最多不超过510次加法计算（如果密钥长度选定为256bit的话，510 = 255*2）；而反过来通过公钥X和基点G是无法轻易的算出私钥x的，只能通过暴力枚举的方式，基本也是不可行的做法。所以从安全性上考虑，私钥和公钥对是成立的，那么如何利用私钥和公钥做加解密呢？

d）加解密过程

加密方是公钥X持有者，现有消息m需要加密。首先，公钥持有方，生成一个随机数字 r，将m生成一个加密点 （rG, m+rX) 发送给解密方。
解密方是私钥x持有者，得到加密点（rG, m+rX) (记作 a,b) 后 ，对b值做如下运算 b – x * a = m + rX – x * rG = m + r * x * G – x*r * G = m，即可得到原文m

即：
Encrypt(m) = (a,b) = (r*G, m + r*X) ==> c
Decrypt(c) = b – x * a = m + r * x * G – x * r * G = m

由于其他的公钥持有人，不知道 r ，也不知道 x，所以无法解密。 而私钥持有人是不需要知道r就能直接解密的，所以r也不需要传播，也就没有被窃取的风险。

e）补充说明

上面的推导过程貌似没有提到素数，其实这里是对曲线理想化的操作，实际上，曲线本身是连续的，而我们基本需要的数据域只是整数（离散的），而且是有限位的整数（虽然有限，也足够多了）。所以在限定整数域的时候，会引入一些素数的能力，以实现同余运算。这里就不多展开了，但素数作为循环群的阶，是保障算法的可行性非常必要的，不能忽略。例如比特币选的素数阶就是最接近2^255的一个大素数。